In Part 1 of the pathfinding blog post series we saw that with empirical engineering one can already design a reasonable and transparent probability estimator essential for improving payment success. However, it has limitations regarding predictability and is not very flexible. Thus, we introduced an alternative estimator that employs a more rigorous mathematical approach to estimate probabilities. This method, formalized in a seminal publication is based on an assumed liquidity distribution within the network and is able to incorporate past learnings about a channel to output gradual success probabilities for payment amounts differing from the ones of previous payments. The essence of this approach is to answer the following question: if I statistically know how channels' balances are distributed, can I make an informed decision about a channel's success probability with or without prior payment knowledge?

Motivation for Bimodal Model

Probability estimation assumes an underlying balance distribution of channels within the network. An example for a distribution would be a random uniform one, which states that picking any channel, we expect to find its local/remote balance in a random position. This assumption was used by the original work on distribution-based probability estimation, due to initial empirical observations and due to its mathematical simplicity.

In preparation for the implementation of a distribution-based estimator, we studied traces of the balance distribution of the Lightning Network using real payment data. By extracting successes and failures for node pairs of a fixed amount (~500 ksat) from mission control we were able to determine the empirical success probability of channels with respect to their capacities, which is shown in the following graph.

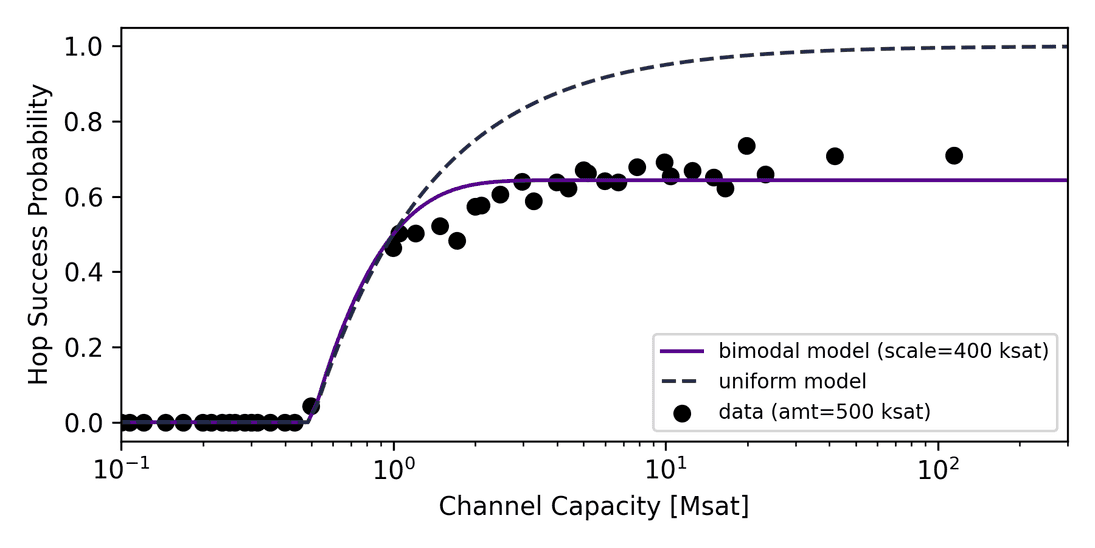
It is helpful to first understand the uniform case. For channel capacities below the payment amount, no channel can route resulting in a zero probability. With growing capacity, payment success is expected to reach unity as we anticipate to always find some leftover balances that can carry the payment. The empirical data however shows that the probability saturates, i.e. is independent of the capacity if the capacity is large compared to the amount, not in line with a uniform distribution. Can we model the distribution differently? It turns out that a distribution that assumes unbalanced channels can describe the situation (confirmed in a recent publication). This distribution assumes that a channel has liquidity either on the local or the remote side, a U-shaped distribution we call bimodal, displayed in the next graph.

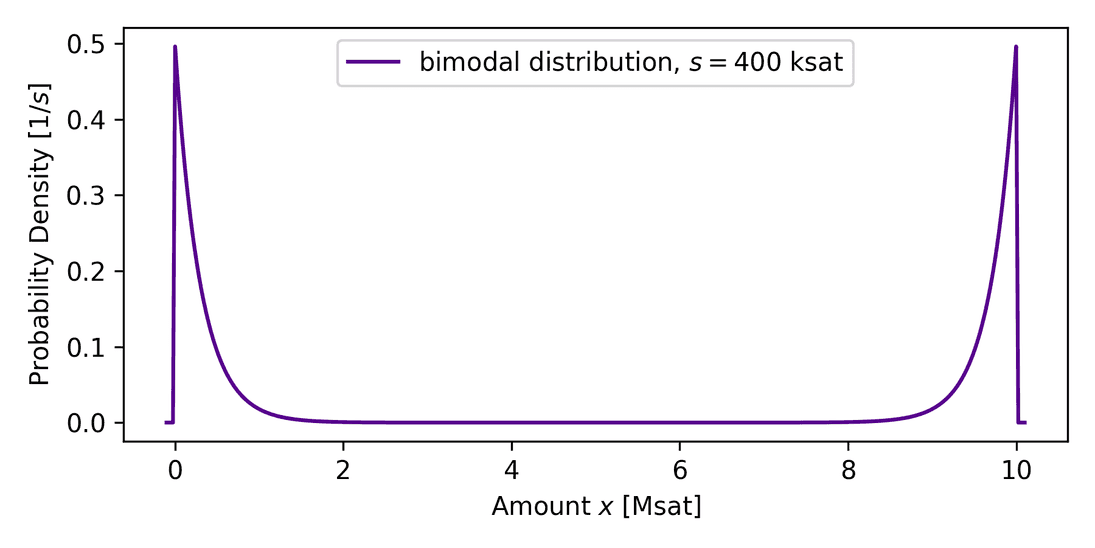
We suspect that liquidity is scattered in this way because it has evolved from unidirectional payment flows from strong sources (wallets) to strong sinks (merchants), together with nodes that charge inappropriate fees for their liquidity which is exploited by rebalancers capturing the liquidity. As there are also channels that are well maintained, or experience backward flow, we expect some uniform or unimodal (balanced channels with around 50:50 distribution) components in the distribution as well.

Implementation and Probability Estimates

To adapt the original research on probability-based routing to unbalanced channels, we devised a new balance distribution model following the formula $P(x) \propto \exp(-x/s) + \exp((x-c)/s)$ up to some normalization constant, the bimodal distribution, shown in the previous graph.

The model describes the probability of finding the balance at amount $x$ in a channel with capacity $c$. For a uniform model, this would be constant, but here the model is composed of two mirrored exponentials that are located at the channel boundaries, which exactly describes situations in which channel liquidity is mostly found on the local or the remote side, but rather not in between. A scale parameter $s$ is added to the model in order to be able to configure how far the balances extend into the channel (we mentioned that there may be backward flow that reestablishes some of the balance).

We derived formulas for unconditional and conditional success probabilities, where the unconditional probability is shown in the graph above. Remarkably, for an amount of 400 ksat, the bimodal success probability describes the situation very well, which hints for unbalanced channel balance distributions.

The conditional success probability depends on previous successes and failures for a specific channel. Should those data points not be available, then the success amount is assumed zero (we always expect to be able to "send" a zero amount) or to be the full capacity (we expect to not be able to send the whole capacity all at once). The following graph demonstrates the power of this approach, which enables smarter decision-making by interpolation of probabilities.

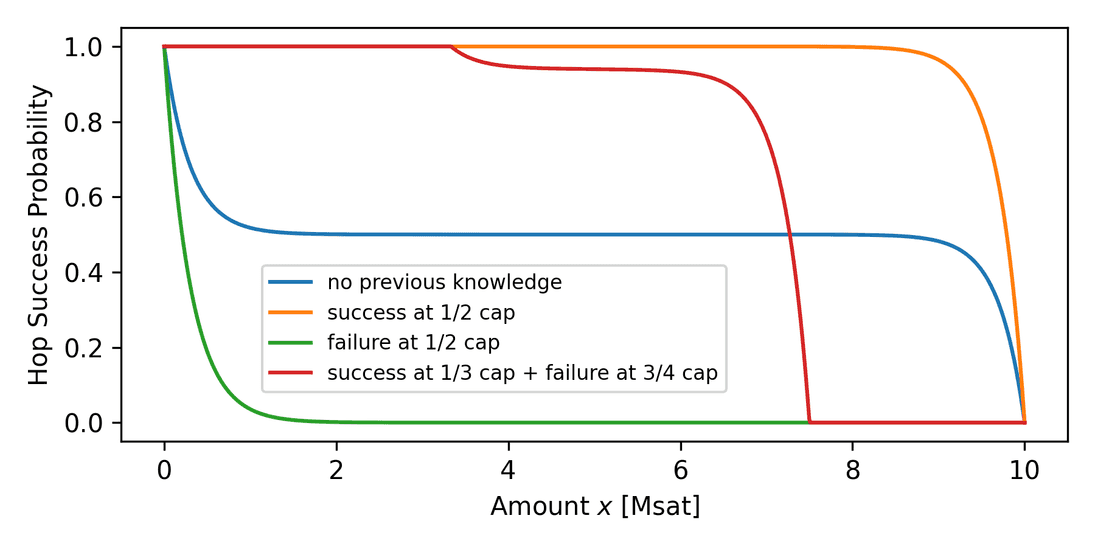
There are four major cases to discuss, see Fig. 6:

1. Unconditional - no previous knowledge: This is the same probability as in Fig. 4 but shown as a function of the amount instead of capacity, which is fixed to 10 Msat here. We expect to be able to send a small amount as the assumption is that we'll always find some small balance left in the channel (on the scale $s$) and further that we can't send close to the full amount as there's always going to be a missing balance.

2. Conditional - previous (unsettled) success: If we learned from a previously failed payment attempt that a hop on the route could forward a certain amount, we'll be able to send this or a lower amount in the next attempt using a modified route. The model tells us that the channel's liquidity can even be used up almost entirely, because we discovered that the channel was unbalanced in the correct direction. Note that this is in contrast to the a priori model, which didn't make any statements about amounts higher than the previous success amount.

3. Conditional - previous failure: If we failed to send over the channel with a relatively large amount (say half the capacity), it's unlikely we can send a lower amount at all, except for very small amounts comparable to the scale $s$.

4. Conditional - success and failure: We can also consider both cases together, successes and failures, which will interpolate success probabilities between the success and failure cases.

Surprisingly, it turns out that the behavior of the bimodal model is very close to the a priori model, the latter being a result of several years of engineering. The most prominent attributes in common are that liquidity is used successively until proven otherwise by a failure and that for intermediate amounts we get a probability close to 50%.

Using this formalism, we can put the knowledge about previous successes and failures to work to make better decisions. However, network conditions change and the information about channels naturally becomes outdated over time. Failed channels could have been healed by backflow or liquidity provisioning and liquid hops could have been used up by other participants. This is why incorporation of knowledge decay is important. We can achieve this by allowing the previous failure and success amounts to gradually return to the zero amount or to the capacity, respectively. In that process we will continuously transform the conditional success probability to the case with no prior knowledge, the speed of which can be controlled with bimodal.decaytime. This time determines how quickly we forget information, currently defaulting to 7 days.

The advantages of the bimodal model compared to the a priori model are that it is mathematically more rigorous and extensible and it is superior in estimating probabilities that are off from previous amounts. It accurately reflects network conditions, but also has a degree of freedom in the scale parameter $s$ to fine tune should conditions change. The scale can also serve to model a uniformly distributed network by selecting a large value compared to prevalent channel sizes. We chose to implement this model as it is similar to the a priori model and thus in line with the current LND pathfinding philosophy of not introducing bias for large channels like a uniform model would do. This helps to spread out traffic across all channels to bolster decentralization and to prevent channel jamming. The shortcomings of both models are a tendency to exhaust channels (one could argue that this is capital efficient) and the bimodal model engages in more aggressive splitting as small parts always have a relatively high success probability. One downside of the bimodal model is that it is not directly suitable for use in min-cost flow solvers. We also note that exponential functions are rather slow to evaluate, which could be remedied by replacement with a polynomial expression. However, the evaluation cost of exponentials is not the bottleneck in LND's pathfinding currently.

Diving Deeper into Gossip Signals

We think that the unconditional unbiasedness concerning channels is important. The philosophy is to rather keep routing fees as the dominant factor. This outsources the problem of liquidity signaling to routers and therefore incentivizes them to solve liquidity problems. In fact, this is already a reality today as depicted in the following graph.

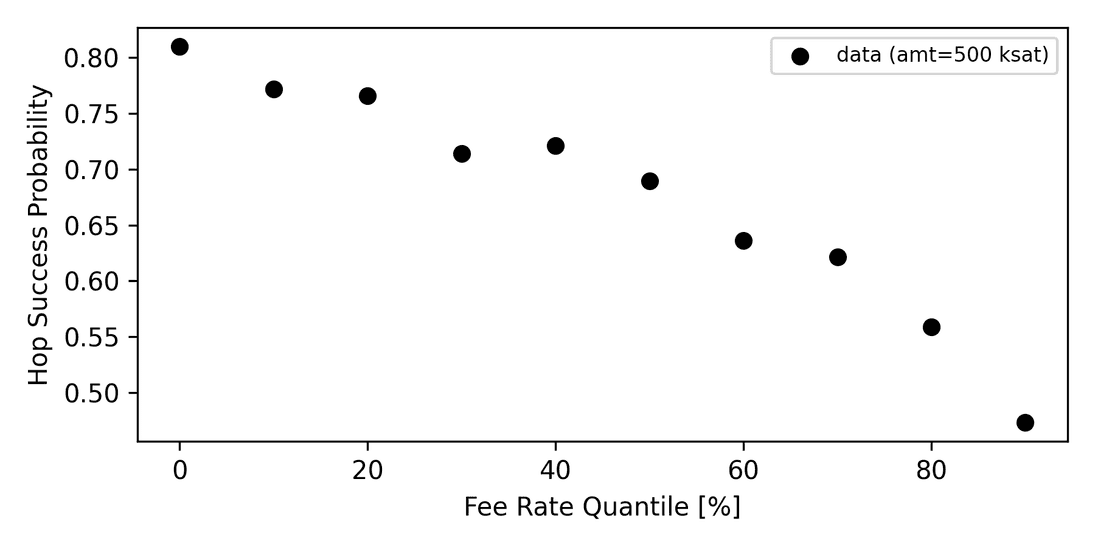
The graph in Fig. 7 shows empirical hop success probabilities based on node-internal relative routing fees of channels. Each channel is assigned a fee rate bucket that classifies the channel as cheap or expensive (the bins spread between min and max fee rates with linear quantile spacing). Averaged success and failure events lead to estimates of success probability with respect to the fee buckets. This figure tells us that routers charge relatively more when liquidity is scarce and they discount unused liquidity. We can see a clear trend of continuously decreasing success probabilities with higher fee rate buckets. This proves that routers indeed steer traffic by fee rate modulation, providing a signal to payers where liquidity can be found. However, today only 10% (2300) of nodes apply this flow control, which is why more education on that topic is necessary to make the Lightning Network more reliable. Setting fees in a reasonable manner enables routing nodes to increase their earnings, thereby contributing to the network's ability to efficiently route payments, creating a symbiotic relationship between pathfinders and routing nodes. In the future, we may witness pathfinding algorithms to penalize nodes that do not adjust their fees. Routers interested in this topic can turn on AutoFees on Terminal.

Outlook

Designing a pathfinding algorithm (and cost function) is complex, judging whether changes lead to improvements is even more so. The bimodal model is currently marked experimental and we need methods to evaluate the general concept as well as to fine tune model parameters to give recommendations for different use cases. One approach could be to employ A/B testing for real payments. For a fair comparison one could alternate between models (lncli setmccfg can be helpful here) and record their respective probability estimates and outcomes. For a direct comparison it is important not to incorporate hints from previous trials. This can be done by saving and restoring mission control data by a chain of calls to QueryMissionControl, ResetMissionCotrol, and ImportMissionControl. Extensions are planned to simplify this process by adding mission control name spacing. An alternative approach would be to simulate payments on a model of the network and its liquidity distribution, however this loses the connection to the specific implementation and to real economics.

Conclusion

Pathfinding algorithms that create the demand together with routers that provide the supply will shape the network in order to improve user experience. In this article series we described how the process of payment planning and pathfinding is carried out in LND. We discussed ingredients that enter a payer's route preference with a focus on success probability estimation. A newly introduced model for distribution-based probability estimation, the bimodal model, provides another degree of freedom for node operators to play with to make pathfinding smarter. We expect this model to be superior compared to the current model, which still needs to be proven by experiments and simulations. We laid out a vision of how the Lightning Network will improve on payment success, namely by a market process between economically rational routing nodes and pathfinders that buy the offered liquidity. We encourage all node operators to join us in this endeavor and to report back on their experience.